
Numerical Modeling of Stratified Flows
We developed an Arbitrary Lagrangian-Eulerian Variational Multi-Scale (ALE-VMS) formulation aimed at the simulation of stratified flows on moving domains. The formulation couples the Navier–Stokes equations of incompressible flows with the Boussinesq approximation, and a scalar advection–diffusion equation for the density or temperature field. The weakly-enforced boundary conditions are also implemented to allow more accurate and efficient computation of the flow near the wall, including the rough walls. The proposed formulation showed good agreement with experimental results and DNS simulations reported by other researchers.

Aerodynamic simulation of atmospheric flow over the Perdigao terrain. Slice of the domain with horizontal velocity.




Simulation of the stratified channel flow at friction Re number of 180 (Left) and 550 (Right) and Ri number of 120 using quadratic NURBS discretization and wall-model based Dirichlet boundary condition. Left-Top: VMS simulation (265x64x256); Left-Middle: DNS (1152x97x1024); Left-Bottom: Comparison in terms of RMS (triangle is DNS with Ri=12, cross - DNS at Ri=120); Right-Top: flow field; Right-Bottom: comparison with DNS. Results in excellent agreement with DNS on even a way coarser meshes.
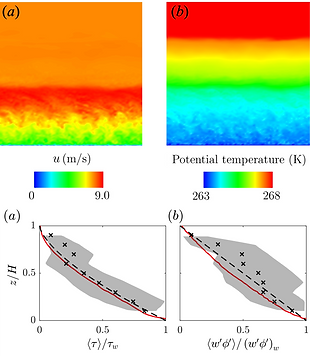
Computation of the stable atmospheric boundary layer from Beaufort Sea Arctic Stratus Experiment (BASE). The wall-function based weak Dirichlet boundary condition with a wall roughness are implemented in a context of VMS and IGA. Results are in excellent agreement with experiment in capturing low-level jets.


Computation of the stratified flow over the 3D hill for different stratification regimes, showing the accuracy in capturing hydraulic jump and different patterns depending on the Fraude number variation.
The framework can be used to understand the dynamic behaviour of the Atmospheric Boundary Layer (ABL) flows with different stability regimes over complex terrain, including hills and mountains; understand the effect of atmospheric stability on wind turbine wake generation and wake-turbine interaction in a context of aerodynamic and FSI analysis of multiple wind turbines; understand turbulent mixing in stratified flows and the effect of stratification on wake collapse.
Publications
-
Y. Bazilevs, K.Takizawa, T.Tezduyar, A.Korobenko, T. Kuraishi, Y. Otoguro
Computational aerodynamics with isogeometric analysis, Journal of Mechanics, 39, pp. 24-39, 2023 -
H. Cen, Q. Zhou, A.Korobenko
Isogeometric variational multiscale modeling of stably stratified flows over complex terrains, Mathematical Models and Methods in Applied Sciences, 32(12), 2371-2399, 2022 -
H. Cen, Q. Zhou, A.Korobenko
Wall-function-based weak imposition of Dirichlet boundary condition for stratified turbulent flows, Computers & Fluids, 234, 105257, 2022 -
H. Cen, Q. Zhou, A.Korobenko
Simulation of stably stratified turbulent channel flow using residual-based variational multiscale method and isogeometric analysis, Computers & Fluids,214, 104765, 2021 -
A.Korobenko, J.Yan, S.M.I.Gohari, S.Sarkar, Y.Bazilevs
FSI Simulations of Multiple Horizontal-Axis Wind Turbines Interacting with Atmospheric Boundary Layer Flow, Computers & Fluids,158, 167-175, 2017 -
J.Yan, A.Korobenko, A.Tejada-Martinez, R.Golshan, Y.Bazilevs
A new variational multiscale formulation for stratified incompressible turbulent flows, Computers & Fluids, 158, 150-156, 2017 -
Y.Bazilevs, A.Korobenko, J.Yan, A.Pal, S.M.I.Gohari, S.Sarkar
ALE-VMS Formulations for Stratified Turbulent Incompressible Flows with Applications, Mathematical Models and Methods in Applied Science, 25(12), 2015
